You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Revealing the Map
- Thread starter version
- Start date
william_kent
Well-known member
It seems like an easy way to ruin things. You could end up breaking down all these great novels into horrible, sterile charts and components until all the life's been drained out of them.
that's called "digital humanities" - "distance reading" of texts as opposed to the old-fashioned "close reading", the production of network diagrams and sentiment analysis ( what percentage of the text is "angry words", etc., )
Something like that was done with Pollock's paintings too, iirc. There's also this from a few years ago,I think that was one of the first applications of textual AI, someone crunching Shakespeare to try to answer whether he had written them all

Scientists find evidence of mathematical structures in classic books
Researchers at Poland’s Institute of Nuclear Physics found complex ‘fractal’ patterning of sentences in literature, particularly in James Joyce’s Finnegans Wake, which resemble ‘ideal’ maths seen in nature
Clinamenic
Binary & Tweed
Again to clarify you can't see personal info like names, you just see from which wallet address, to which wallet address, etc.But yeah go to blockchain.com and you can see every bitcoin transaction ever made. From whom, to whom, how much, and when.
Pollock is only amazing cos he actually ate picassoSomething like that was done with Pollock's paintings too, iirc. There's also this from a few years ago,

Scientists find evidence of mathematical structures in classic books
Researchers at Poland’s Institute of Nuclear Physics found complex ‘fractal’ patterning of sentences in literature, particularly in James Joyce’s Finnegans Wake, which resemble ‘ideal’ maths seen in naturewww.theguardian.com
Clinamenic
Binary & Tweed
Blockchain is still more profound to me than what I understand of machine learning, although really its a toss-up.
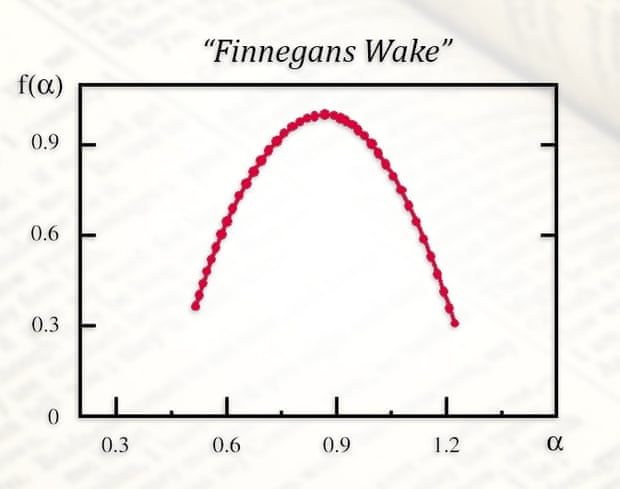
James Joyce’s Finnegans Wake has been described as many things, from a masterpiece to unreadable nonsense. But it is also, according to scientists at the Institute of Nuclear Physics in Poland, almost indistinguishable in its structure from a purely mathematical multifractal.
The academics put more than 100 works of world literature, by authors from Charles Dickens to Shakespeare, Alexandre Dumas, Thomas Mann, Umberto Eco and Samuel Beckett, through a detailed statistical analysis. Looking at sentence lengths and how they varied, they found that in an “overwhelming majority” of the studied texts, the correlations in variations of sentence length were governed by the dynamics of a cascade – meaning that their construction is a fractal: a mathematical object in which each fragment, when expanded, has a structure resembling the whole.
[...]
“All of the examined works showed self-similarity in terms of organisation of the lengths of sentences. Some were more expressive – here The Ambassadors by Henry James stood out – others to far less of an extreme, as in the case of the French 17th-century romance Artamene ou le Grand Cyrus. However, correlations were evident, and therefore these texts were the construction of a fractal,” said Dr Paweł Oświęcimka from the Institute of Nuclear Physics of the Polish Academy of Sciences, one of the authors of the new paper Quantifying Origin and Character of Long-range Correlations in Narrative Texts.
Some works, however, were more mathematically complex than others, with stream-of-consciousness narratives the most complex, comparable to multifractals, or fractals of fractals. Finnegans Wake, the scientists found, was the most complex of all.
“The absolute record in terms of multifractality turned out to be Finnegans Wake by James Joyce. The results of our analysis of this text are virtually indistinguishable from ideal, purely mathematical multifractals,” said Professor Stanisław Drożdż, another author of the paper, which has just been published in the computer science journal Information Sciences.
The academics put more than 100 works of world literature, by authors from Charles Dickens to Shakespeare, Alexandre Dumas, Thomas Mann, Umberto Eco and Samuel Beckett, through a detailed statistical analysis. Looking at sentence lengths and how they varied, they found that in an “overwhelming majority” of the studied texts, the correlations in variations of sentence length were governed by the dynamics of a cascade – meaning that their construction is a fractal: a mathematical object in which each fragment, when expanded, has a structure resembling the whole.
[...]
“All of the examined works showed self-similarity in terms of organisation of the lengths of sentences. Some were more expressive – here The Ambassadors by Henry James stood out – others to far less of an extreme, as in the case of the French 17th-century romance Artamene ou le Grand Cyrus. However, correlations were evident, and therefore these texts were the construction of a fractal,” said Dr Paweł Oświęcimka from the Institute of Nuclear Physics of the Polish Academy of Sciences, one of the authors of the new paper Quantifying Origin and Character of Long-range Correlations in Narrative Texts.
Some works, however, were more mathematically complex than others, with stream-of-consciousness narratives the most complex, comparable to multifractals, or fractals of fractals. Finnegans Wake, the scientists found, was the most complex of all.
“The absolute record in terms of multifractality turned out to be Finnegans Wake by James Joyce. The results of our analysis of this text are virtually indistinguishable from ideal, purely mathematical multifractals,” said Professor Stanisław Drożdż, another author of the paper, which has just been published in the computer science journal Information Sciences.

Clinamenic
Binary & Tweed
sus
Moderator
I feel like there are moves authors make which rely on previous moves, such that if you aren't familiar with those previous moves, you don't "get" it
And there are also moves authors make which recapitulate previous moves, making the originals redundant, such that if you've read the later work, there's no need for the earlier
And there are also moves authors make which recapitulate previous moves, making the originals redundant, such that if you've read the later work, there's no need for the earlier
Clinamenic
Binary & Tweed
If its not open-source, then you are merely trusting the programmers, which isn;t much of a step forward from our current arrangement, in terms of how trust can be exploited and how such exploitation can go unaccounted for.
Organic Intelligence?AI will eat what immediately preceded it.
Depends what your motivation for reading the originals is.And there are also moves authors make which recapitulate previous moves, making the originals redundant, such that if you've read the later work, there's no need for the earlier
Clinamenic
Binary & Tweed
I think AI will be a sort of exostructure for organic intelligence.
What if you saw all those moves somehowI feel like there are moves authors make which rely on previous moves, such that if you aren't familiar with those previous moves, you don't "get" it
And there are also moves authors make which recapitulate previous moves, making the originals redundant, such that if you've read the later work, there's no need for the earlier
No, it could never be. That's a red herring.Organic Intelligence?
I mean that whatever takes over us next must contain what has immediately captivated us before.
Or at least that is what happened with video and Internet.
Certainly I'm most interested in the AI videos rather than the finished single frame.
luka
Well-known member
I've never read a book but I can relate in terms of music. Like Barty can't understand the point of hardcore or enjoy it cos he hears it as primitive jungle, jungle that hasn't self actualised yet. But I dont hear it that way cos I heard it before jungle existedDepends what your motivation for reading the originals is.
What I like now about reading novels written in the nineteenth century is that they could literally be written nowI've never read a book but I can relate in terms of music. Like Barty can't understand the point of hardcore or enjoy it cos he hears it as primitive jungle, jungle that hasn't self actualised yet. But I dont hear it that way cos I heard it before jungle existed
luka
Well-known member
Go on....What I like now about reading novels written in the nineteenth century is that they could literally be written now
Just what I wrote in the French thread. Me and thirdform are having a sort of pedestrian discussion about why new so called exciting music is actually rubbish and then yoh open a book which is 100 years old and a different language and it's all there anc it's uncanny how close it is
